Moore space (topology)

In mathematics, more specifically point-set topology, a Moore space is a developable regular Hausdorff space. Equivalently, a topological space X is a Moore space if the following conditions hold:

• Any two distinct points can be separated by neighbourhoods, and any closed set and any point in its complement can be separated by neighbourhoods. (X is a regular Hausdorff space.)
• There is a countable collection of open covers of X, such that for any closed set C and any point p in its complement there exists a cover in the collection such that every neighbourhood of p in the cover is disjoint from C. (X is a developable space.)

Moore spaces are generally interesting in mathematics because they may be applied to prove interesting metrization theorems. The concept of a Moore space was formulated by R. L. Moore in the earlier part of the 20th century.

Examples and properties

1. Every metrizable space, X, is a Moore space. If {A_x} is an open cover of X (indexed by X) by all balls of radius 1/n, then the collection of all such open covers as n varies over the positive integers is a development of X. Since all metrizable spaces are normal, all metric spaces are Moore spaces.
2. Moore spaces are a lot like regular spaces and different to normal spaces in the sense that every subspace of a Moore space is also a Moore space.
3. The image of a Moore space under an injective, continuous open map is always a Moore space. Note also that the image of a regular space under an injective, continuous open map is always regular.
4. Both examples 2 and 3 suggest that Moore spaces are a lot similar to regular spaces.
5. Neither the Sorgenfrey line nor the Sorgenfrey plane are Moore spaces because they are normal and not second countable.
6. The Moore plane (also known as the Niemytski space) is an example of a non-metrizable Moore space.
7. Every metacompact, separable, normal Moore space is metrizable. This theorem is known as Traylor’s theorem.
8. Every locally compact, locally connected space, normal Moore space is metrizable. This theorem was proved by Reed and Zenor.
9. If 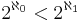, then every separable normal Moore space is metrizable. This theorem is known as Jones’ theorem.

History

For a long time, topologists were trying to prove the so-called normal Moore space conjecture: every normal Moore space is metrizable. This was inspired by the fact that all known Moore spaces that were not metrizable were also not normal. This would have been a nice metrization theorem. There were some nice partial results at first; namely properties 7, 8 and 9 as given in the previous section.

Here we see that we drop metacompactness from Traylor's theorem, but at the cost of a set-theoretic assumption. Another example of this is Fleissner's theorem that the axiom of constructibility implies that locally compact, normal Moore spaces are metrizable.

On the other hand, under the Continuum hypothesis (CH) and also under Martin's Axiom and not CH, there are several examples of non-metrizable normal Moore spaces. Finally, Nyikos settled the matter: the conjecture is independent of ZFC. Under the so-called PMEA (Product Measure Extension Axiom), which needs a large cardinal, all normal Moore spaces are metrizable. Moreover, it was shown later that any model of ZFC in which the conjecture holds, implies the existence of a model with a large cardinal. So large cardinals are needed essentially.

Moore himself proved the theorem that a collectionwise normal Moore space is metrizable, so strengthening normality is another way to settle the matter.

References

• Lynn Arthur Steen and J. Arthur Seebach, Counterexamples in Topology, Dover Books, 1995. ISBN 0-486-68735-X
• This article incorporates material from Moore space on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
• The original definition by R.L. Moore appears here:

MR0150722 (27 #709) Moore, R. L. Foundations of point set theory. Revised edition. American Mathematical Society Colloquium Publications, Vol. XIII American Mathematical Society, Providence, R.I. 1962 xi+419 pp. (Reviewer: F. Burton Jones)

• Historical information can be found here:

MR0199840 (33 #7980) Jones, F. Burton "Metrization". American Mathematical Monthly 73 1966 571–576. (Reviewer: R. W. Bagley)

• Historical information can be found here:

MR0203661 (34 #3510) Bing, R. H. "Challenging conjectures". American Mathematical Monthly 74 1967 no. 1, part II, 56–64;

• Vickery's theorem may be found here:

MR0001909 (1,317f) Vickery, C. W. "Axioms for Moore spaces and metric spaces". Bulletin of the American Mathematical Society 46, (1940). 560–564